f-Divergence DRO¶
[3]:
import numpy as np
# Prepare Data
from dro.data.dataloader_regression import regression_basic
from dro.data.dataloader_classification import classification_basic
from dro.data.draw_utils import draw_classification
X, y = classification_basic(d = 2, num_samples = 100, radius = 2, visualize = True)
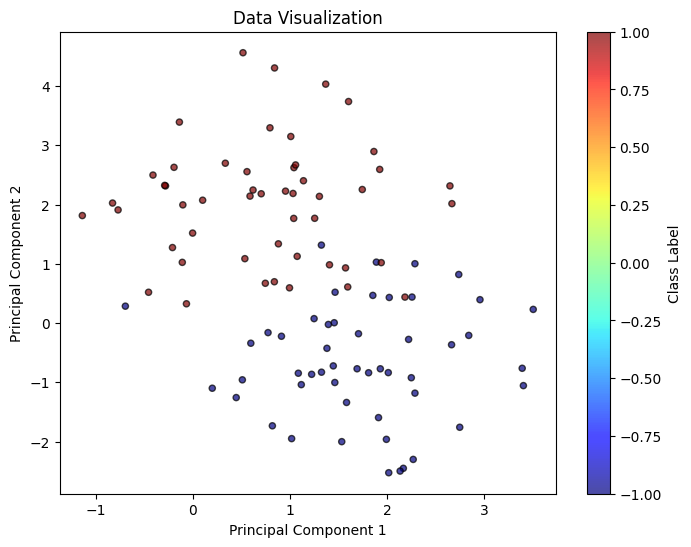
Standard f-divergence DRO¶
We include chi2, cvar, kl, tv distance, which corresponds to the standard definition of (generalized) f-divergence.
The following steps including model fitting, and worst-case illustrations.
[5]:
from dro.linear_model.chi2_dro import *
from dro.linear_model.cvar_dro import *
from dro.linear_model.tv_dro import *
from dro.linear_model.kl_dro import *
clf_model_chi2 = Chi2DRO(input_dim=2, model_type = 'logistic')
clf_model_cvar = CVaRDRO(input_dim=2, model_type = 'logistic')
clf_model_kl = KLDRO(input_dim = 2, model_type = 'logistic')
clf_model_tv = TVDRO(input_dim = 2, model_type = 'logistic')
[6]:
## model fitting
clf_model_chi2.update({'eps': 1})
print(clf_model_chi2.fit(X, y))
clf_model_kl.update({'eps': 1})
print(clf_model_kl.fit(X, y))
clf_model_tv.update({'eps': 0.3})
print(clf_model_tv.fit(X, y))
clf_model_cvar.update({'alpha':0.8})
print(clf_model_cvar.fit(X, y))
{'theta': [-0.6347179732189498, 1.9680342006517346], 'b': array(-0.51071442)}
{'theta': [-0.21802718101618923, 0.7358683074228745], 'dual': 0.16652943997935335, 'b': array(-0.233648)}
{'theta': [-0.17601214229950132, 1.258840209573551], 'threshold': array(0.094178), 'b': array(-0.79542609)}
{'theta': [-1.3466023842845223, 3.823698339513048], 'threshold': array(0.00019594), 'b': array(-0.7506087)}
[7]:
# worst case distribution for each method
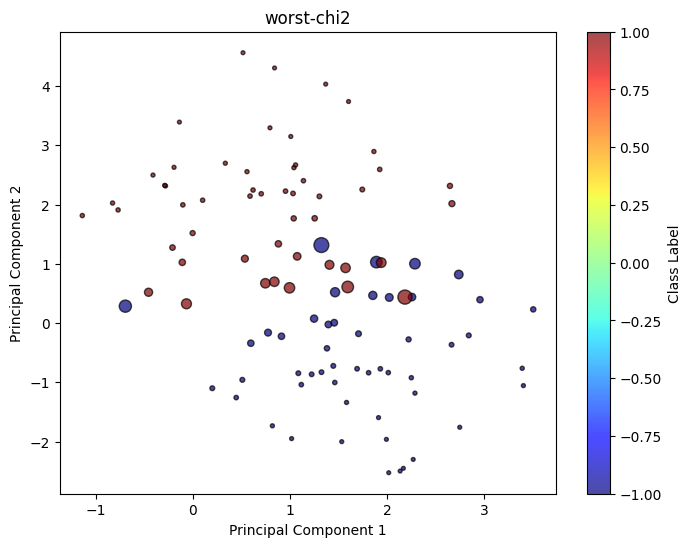
worst_chi2 = clf_model_chi2.worst_distribution(X, y)
draw_classification(worst_chi2['sample_pts'][0], worst_chi2['sample_pts'][1], weight = worst_chi2['weight'], title = 'worst-chi2')
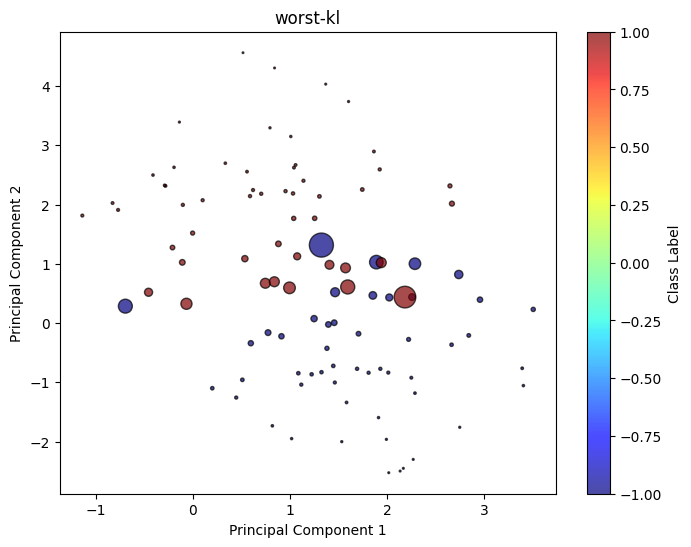
worst_kl = clf_model_kl.worst_distribution(X, y)
draw_classification(worst_kl['sample_pts'][0], worst_kl['sample_pts'][1], weight = worst_kl['weight'], title = 'worst-kl')
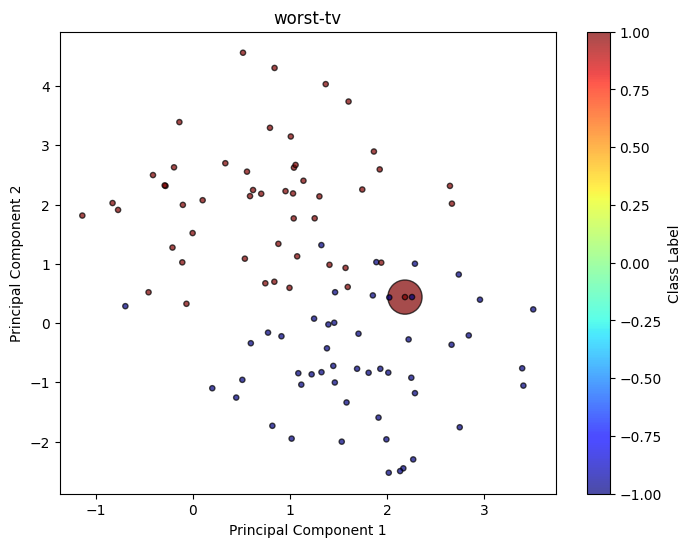
worst_tv = clf_model_tv.worst_distribution(X, y)
draw_classification(worst_tv['sample_pts'][0], worst_tv['sample_pts'][1], weight = worst_tv['weight'], title = 'worst-tv')
worst_cvar = clf_model_cvar.worst_distribution(X, y)
draw_classification(worst_cvar['sample_pts'][0], worst_cvar['sample_pts'][1], weight = worst_cvar['weight'], title = 'worst-cvar')
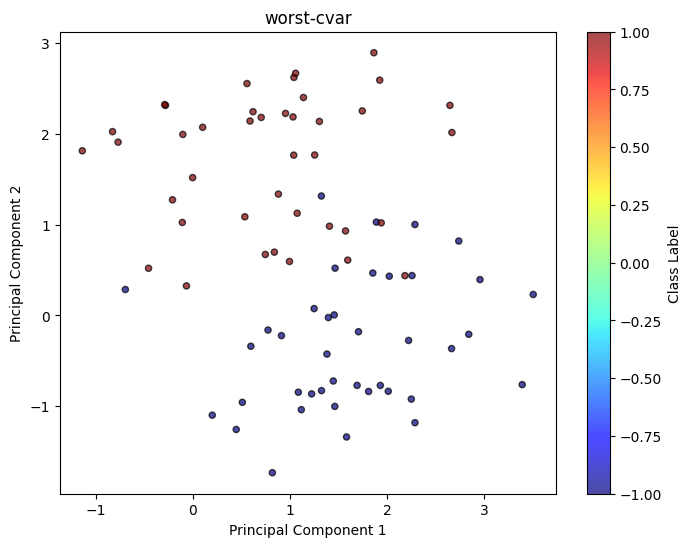
data driven evaluation¶
[8]:
import numpy as np
from sklearn.datasets import make_regression
from dro.linear_model.chi2_dro import *
# Data generation
sample_num = 200
X, y = make_regression(n_samples = sample_num, n_features=10, noise = 5, random_state=42)
eps = 2 / sample_num
dro_model = Chi2DRO(input_dim = 10, model_type = 'ols', fit_intercept=False)
dro_model.update({'eps': 0.5})
dro_model.fit(X, y)
dro_model.evaluate(X, y)
[8]:
24.763974457342453
[9]:
errors = (dro_model.predict(X) - y) ** 2
np.mean(errors)
[9]:
24.05810847832465
These f-divergence DROs are suitable for handling general distribution shifts with likelihood misspecification, while can be too worst-case in practice.
Partial Distribution Shift¶
Some special kinds of DRO models can help handle problems of particular worst-case distribution shift, i.e., covariate shift (marginal_dro). Both of them are built from CVaR-DRO.
[10]:
from dro.linear_model.conditional_dro import *
from dro.linear_model.marginal_dro import *
from dro.data.dataloader_classification import classification_basic
X, y = classification_basic(d = 2, num_samples = 100, radius = 2, visualize = True)
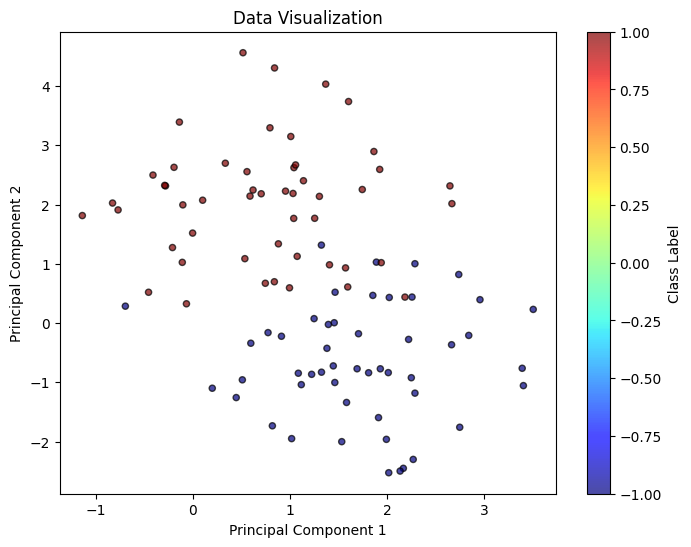
[14]:
clf_model_margin = MarginalCVaRDRO(input_dim = 2, model_type = 'svm')
clf_model_cond = ConditionalCVaRDRO(input_dim = 2, model_type = 'logistic')
clf_model_margin.update({'alpha': 0.8})
clf_model_cond.update({'alpha': 0.4})
print('marginal', clf_model_margin.fit(X, y)['theta'])
print('conditional', clf_model_cond.fit(X, y))
marginal [-1.1801401031360952, 2.3632113317955987]
conditional {'theta': [-1.2843606942632635, 3.5303014542999374], 'b': array(-0.64246721)}
/Users/jiashuo/anaconda3/envs/llm-ot/lib/python3.10/site-packages/cvxpy/expressions/expression.py:674: UserWarning:
This use of ``*`` has resulted in matrix multiplication.
Using ``*`` for matrix multiplication has been deprecated since CVXPY 1.1.
Use ``*`` for matrix-scalar and vector-scalar multiplication.
Use ``@`` for matrix-matrix and matrix-vector multiplication.
Use ``multiply`` for elementwise multiplication.
This code path has been hit 4 times so far.
warnings.warn(msg, UserWarning)